The Black Ink Team's Guide To Statistical Distributions
by Black Ink Team
Statistics is the process of collecting large amounts of data and using it to produce probability models. Say you had a coin, and you wanted to test the probability of flipping it heads or tails. You would first flip it a bunch of times and record the results. Using statistics you could deduce the probability of it landing on either side, as well as calculate how accurate your test was. You could also find out whether different combinations (heads after heads after tails, for example) are more likely to show up than others. A statistical distribution is an idealized version of experimental results that you use to weigh the consistency of your observations. They are usually shown as graphs but each can be expressed in algebraic terms.
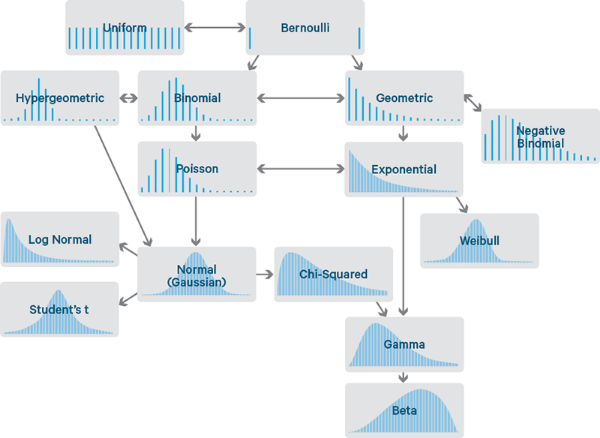
An easy way to pick the right distribution to use would be to graph your results over a few, to see whether your data lines up with one. But you can also narrow down which distribution you need by asking yourself a few questions about your data. Every statistical distribution is designed to model certain types of data. Data differs from other data in many ways - it can be discrete or continuous, it can be symmetric or asymmetric, it can have many outliers or almost none, etc. Discrete data can only be a set number of values (i.e. heads/tails, yes/no, and pass/fail) whereas continuous data can fall anywhere within a range. Symmetric data describes a curve that has similar slopes on either sides, whereas asymmetric data is skewed to the left or right. Outliers are points that fall way outside the main cluster of data, and can signify that an experiment was flawed. In a normal distribution, outliers fall on the 'tails' which are infinitely long, seemingly flat but actually sloping areas of the graph on either side, which is why highly unlikely results are sometimes referred to as 'long-tail.'
Here are some examples of statistical distributions along with reasons why you would want to use them:
Binomial: Your data is discrete, you can't estimate results, it is symmetric, and the points gather around one value
Geometric: Your data is discrete, you can't estimate results, it is asymmetric, and the outliers are only positive
Uniform: Your data is continuous, it is symmetric, and the points do not gather around one value
Normal: Your data is continuous, it is symmetric, the points gather around one value, and there are very few outliers
Exponential: Your data is continuous, it is asymmetric, and the outliers are only positive